Introduction

This is a writeup of the Parking challenge of the GoogleCTF 2021

Challenge Description

It's so crowded today... Can you fit our car in?

Attachments: game.py, level1, level2 and run.sh

Solution

So after starting the first level, we are greeted with this matplotlib diagram:

python game.py level1

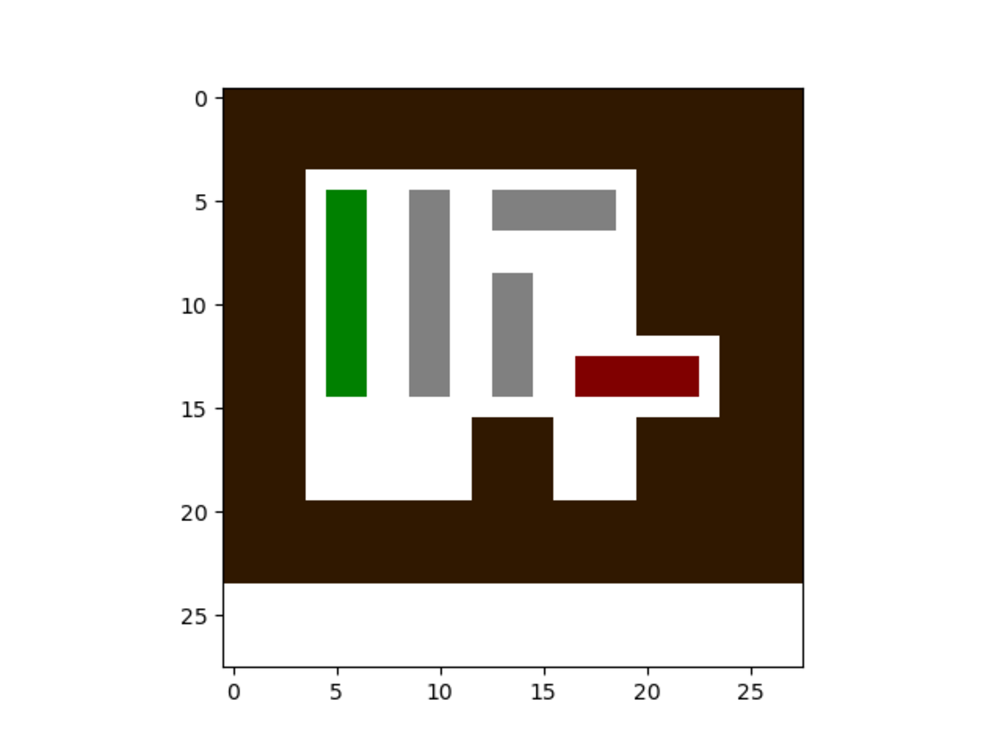
This is actually a game that can be played by clicking inside the diagram.

The green, grey and red boxes represent cars. They can be moved only forward and backward (apparently driving wheels were not invented yet). The goal of the game is to arrange the car in a way that allows the red car to move. This is actually very similar to the principle of this Android game "Unblock Me"

The position of the green car(s) is then used to calculate the flag. Level 1 was only for demonstration of the rules. Level 2 is the real challenge, so let's fire that up

python game.py level2

Well ok, this is slightly more complicated. If you zoom in more you can still see the individual cars though, so it should not be that complicated.

We did know that this challenge can be solved with a tool like z3, but we realized that there are a lot of similar patterns throughout the entire "parking lot". Also we were amazed by the idea of building logic gates out of cars, so we started examining:

Something we noticed is that the red car is in the lower right corner of the plane, while all the green cars are at the very left. Also the entire structure has their components replicated 64 times vertically. There are also exactly 64 green cars, which have only two positions to be in. This means our input is a 64 bit number which we apply some logic on to derive wether their position allows the red car to move or not.

Basic Components and Gates

Let's dig into the basic components. At the smalest scale we have:

component	explanation
	or gate: either car can move out of the way to allow the ouput car to move
	and gate: both cars need to move to allow the ouput car to move
	splitter: if an and gate is used in the other direction, we get a signal splitter
	crossing: both chains (top to bottom and left to right) can independently carry their signal
	constant: a constant is represented via a dead end wich either allows the car to move or not

Higher Level Gates

The reason a constant always consists of two opposing strands is very simple: In order to force the green cars into a certain position, the challenge authors had to consider both cases (car up or car down) and apply logic to it. If only one position was checked, we could just move all cars in the opposite position and get a valid solution to the puzzle, but not the intended flag. So actually the entire higher level logic always has two opposing strands for every signal.

From the basic components we recognized before, some more advanced logic blocks were created:

component	explanation
	xor gate: this gate first calculates all combinations of the four inputs (remember that the inputs a and a always come as two opposing "wires". from top to bottom we have a, ¬a, b and ¬b.The output XOR is then computed as (a AND ¬b) OR (¬a AND b). Because this is a higher level component, all calculations have to be done twice, so the negative strand is calculated as (a AND b) OR (¬a AND ¬b)
	half adder: similarly to the xor gate, but it additionally performs the calculaiton of the carry bit as (a AND b) with the respective negative strand

The Big Picture (literally)

We can now reconstruct what the entire circuit does. If we take three of the 64 rows, the circuit looks like this:

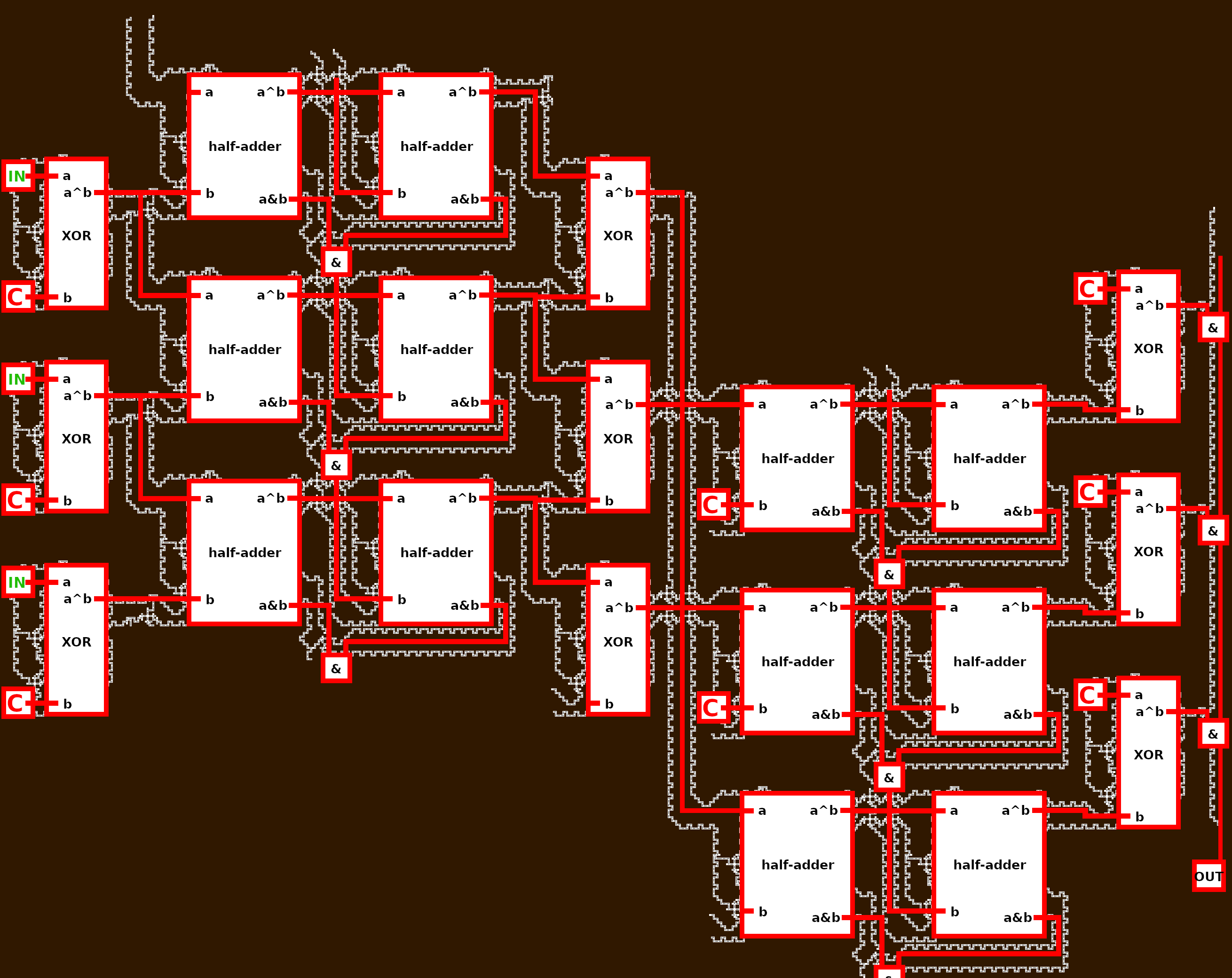
(Note: all the inputs that are not connected just lead to zero constants)

We can see that the half adders always form a full adder. So the entire circuit performs the following operations:

1. XOR with a 64-bit constant
2. Multiply with 3 by adding the value to itself shifted by one (x + (x<<1) == x * 3)
3. XOR with the current value shifted by 1 (x ^ (x>>1))
4. Rotate right by one (ROR x)
5. Add a 64-bit constant
6. XOR with a 64-bit constant
7. And all bits of the current value

The result of those operations needs to be 0. So we only had to write a little scirpt that extracted all the constants and calculated backwards to get the position of the cars. This took some time, but at the end it did work and we could recover the flag using the code from the game.py file. Turns out the 64-bit input value it is just ASCII encoded text

Flag

CTF{2TheBr1m}

Files

sovle.py

import sys
import time
import string
from PIL import Image, ImageDraw
from matplotlib import pyplot as plt
if sys.platform == 'darwin':
    import matplotlib
    matplotlib.use('TkAgg')
import os
import numpy as np
def bitstoint(bits):
    return int(''.join(str(x) for x in bits[::-1]), 2)
def bitstostr(bits):
    return ''.join(str(x) for x in bits[::-1])
def inttobits(i):
    return [int(x) for x in "{0:064b}".format(i)[::-1]]
def inttostr(i):
    return "{0:064b}".format(i)
assert bitstoint(inttobits(123456)) == 123456
pic = Image.open("big.png")
data = np.array(pic)
starts = [[2301,805], [1509,1285], [21,805]]
rowsize = 1237 - 805
rows = 64
consts = [[] for _ in range(len(starts))]
for i, var64 in enumerate(starts):
    for row in range(rows):
        x = var64[0]
        y = var64[1]+row*rowsize
        assert data[y][x][2] in [0, 255]
        bit = data[y][x][2] == 0
        consts[i].append(int(bit))
carry = 0
sub1 = []
for i in range(64):
    in1 = consts[0][i] ^ consts[1][i] ^ carry
    sub1.append(in1)
    carry = int(consts[1][i] + carry + in1 >= 2)
sub1i = bitstoint(sub1)
sub1i_fast = bitstoint(consts[0]) - bitstoint(consts[1])
assert sub1i == sub1i_fast
rol1 = sub1[-1:] + sub1[:-1]
carry = 0
xor2 = []
for i in range(64)[::-1]:
    in1 = rol1[i] ^ carry
    xor2.append(in1)
    carry = in1
xor2 = xor2[::-1]
carry = 0
in1 = 0
sub2 = []
for i in range(64):
    in2 = in1 ^ xor2[i] ^ carry
    sub2.append(in2)
    carry = int(carry + in1 + in2 >= 2)
    in1 = in2
sub2i = bitstoint(sub2)
sub2i_fast = (bitstoint(xor2) + 2**64) / 3
assert inttobits((sub2i * 3) % (2**64))  == xor2
res = [x ^ y for x,y in zip(sub2, consts[2])]
def printflag(res):
    bits = ''.join(str(x) for x in res)
    flag = b"CTF{"
    while bits:
        byte, bits = bits[:8], bits[8:]
        flag += bytes([ int(byte[::-1], 2) ])
    flag += b"}"
    print(flag)
printflag(res)